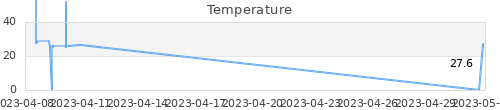
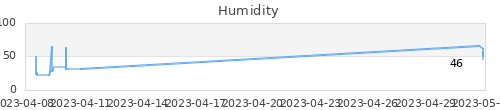
K-MOOC, 센서 및 구동기, 1-2멤스센서 선택
게이지 팩터(Gage Factor, GF)의 일반적인 식은 저항 변화와 변형률의 관계를 나타내는 공식입니다. 이를 유도하기 위해 저항 변화의 주요 요인을 고려해야 합니다.
🔎 게이지 팩터의 기본 정의
게이지 팩터는 변형률(스트레인)에 따른 저항 변화율을 나타냅니다:
[
GF = \frac{\Delta R / R}{\epsilon}
]
여기서:
- ( \Delta R ) = 저항의 변화량
- ( R ) = 초기 저항값
- ( \epsilon ) = 변형률( ( \epsilon = \Delta L / L ))
저항 변화는 두 가지 주요 요인에 의해 결정됩니다:
- 기하학적 변화
- 변형률에 의해 도선의 길이 ( L ) 이 증가하면, 저항은 다음과 같이 변합니다:
[
R = \rho \frac{L}{A}
] - 여기서 ( A ) 는 단면적, ( \rho ) 는 고유 저항(resistivity)입니다.
- 변형 시 도선이 얇아지므로 단면적 변화도 고려해야 합니다.
- 고유 저항(resistivity)의 변화
- 변형에 의해 재료의 미세 구조가 변화하여 고유 저항이 변할 수 있습니다.
- 이 영향을 고려하면 일반적인 식을 유도할 수 있습니다.
📌 일반적인 유도 과정
저항 변화율을 변형률과 관련시켜 계산하면:
[
\frac{\Delta R}{R} = (1 + 2\mu) \epsilon + \frac{\Delta \rho}{\rho}
]
여기서 ( \mu ) 는 푸아송 비(Poisson’s ratio)로, 변형 시 재료의 횡방향 변화율을 나타냅니다.
따라서 게이지 팩터의 일반적인 식은:
[
GF = (1 + 2\mu) + \frac{\Delta \rho / \rho}{\epsilon}
]
이 식은 재료의 기하학적 변화 + 고유 저항 변화를 모두 포함하여 보다 일반적인 형태로 유도됩니다.
이해가 되셨나요? 더 깊이 알고 싶다면 특정 부분을 요청해주세요! 😊🚀
좋아요! 저항 변화율 (\frac{\Delta R}{R}) 의 유도 과정을 정확히 설명해볼게요.
🔹 저항과 변형률의 관계
저항은 다음과 같이 정의됩니다:
[
R = \rho \frac{L}{A}
]
여기서:
- ( R ) = 저항
- ( \rho ) = 고유 저항(resistivity)
- ( L ) = 도선의 길이
- ( A ) = 도선의 단면적
이제 도선이 변형될 때, 길이와 단면적이 변화하면서 저항도 변합니다.
🔹 저항 변화율 계산
변형이 발생하면 길이와 단면적의 변화율을 고려해야 합니다. 이를 미분하여 상대 변화율을 구해봅니다.
[
\frac{\Delta R}{R} = \frac{\Delta \rho}{\rho} + \frac{\Delta L}{L} – \frac{\Delta A}{A}
]
여기서 푸아송 비(Poisson’s ratio) ( \mu ) 를 이용하면 단면적 변화율을 표현할 수 있습니다:
[
\frac{\Delta A}{A} = 2\mu \frac{\Delta L}{L}
]
따라서 위 식을 다시 정리하면:
[
\frac{\Delta R}{R} = \frac{\Delta \rho}{\rho} + (1 + 2\mu) \epsilon
]
여기서 변형률(스트레인) ( \epsilon ) 을 ( \frac{\Delta L}{L} ) 로 표현할 수 있습니다.
🔹 최종 유도 결과: 게이지 팩터
게이지 팩터(GF)는 저항 변화율을 변형률로 나눈 값이므로:
[
GF = \frac{\Delta R / R}{\epsilon} = (1 + 2\mu) + \frac{\Delta \rho / \rho}{\epsilon}
]
이 식은 기하학적 변화(1+2μ)와 재료의 고유 저항 변화((\frac{\Delta \rho}{\rho}))를 모두 고려한 결과입니다.
이해가 되었나요? 혹시 특정 부분이 궁금하면 더 자세히 설명해드릴게요! 😊🚀
좋은 질문이에요! (1 + 2\mu) 항은 변형률이 저항 변화에 미치는 기하학적 효과를 나타냅니다. 이를 이해하려면 길이 변화와 단면적 변화가 저항에 미치는 영향을 분석해야 합니다.
🔹 길이 증가와 저항 증가 ((1) 항)
저항은 다음과 같은 공식으로 표현됩니다:
[
R = \rho \frac{L}{A}
]
- 변형률 ( \epsilon ) 이 도선에 가해지면, 길이 ( L ) 이 증가합니다.
- 길이가 증가하면, 저항도 증가합니다.
- 길이는 변형률과 정비례하므로, 저항 변화율에 (1) 항이 포함됩니다.
즉, 길이 변화만 고려하면 저항은 ( (1) ) 만큼 증가합니다.
🔹 단면적 감소와 저항 증가 ((2\mu) 항)
변형이 발생하면, 도선이 길어지면서 단면적이 줄어들게 됩니다.
이때 푸아송 비(Poisson’s ratio) ( \mu ) 를 사용하여 단면적 변화를 표현할 수 있습니다.
- 푸아송 비 ( \mu ) 는 가로 방향 변형률과 세로 방향 변형률의 비율을 나타냅니다.
- 도선이 늘어나면서 폭이 줄어드므로, 단면적 변화율은 다음과 같이 표현됩니다:
[
\frac{\Delta A}{A} = 2\mu \epsilon
]
- 단면적이 감소하면 저항이 증가하므로, 저항 변화율에 (2\mu) 항이 추가됩니다.
🔹 최종 결과: (1 + 2\mu)
이제 저항 변화율을 전체적으로 보면:
[
\frac{\Delta R}{R} = \frac{\Delta \rho}{\rho} + (1 + 2\mu) \epsilon
]
즉:
- 길이 변화로 인해 저항이 (1) 만큼 증가
- 단면적 감소로 인해 저항이 (2\mu) 만큼 추가 증가
따라서 기하학적 변화에 의해 저항이 변형률의 (1 + 2\mu) 배만큼 증가하는 것입니다.
이해가 되셨나요? 혹시 더 깊이 알고 싶다면 특정 부분을 요청해주세요! 🚀😊좋은 질문이에요! 단면적 변화율 (\frac{\Delta A}{A}) 가 어떻게 ( 2\mu \epsilon )이 되는지 자세히 설명해볼게요.
🔹 푸아송 비(Poisson’s Ratio)와 단면적 변화
푸아송 비 ( \mu ) 는 가로 방향 변형률과 세로 방향 변형률의 비율을 나타냅니다:
[
\mu = – \frac{\epsilon_{\perp}}{\epsilon_{\parallel}}
]
여기서:
- ( \epsilon_{\parallel} ) = 길이 방향 변형률 (( \epsilon = \frac{\Delta L}{L} ))
- ( \epsilon_{\perp} ) = 가로 방향 변형률 (( \epsilon_{\perp} = \frac{\Delta w}{w} ))
즉, 물체가 늘어나면 가로 방향으로 줄어들며, 이 감소량을 푸아송 비 ( \mu ) 가 나타내는 것입니다.
🔹 단면적 변화율 계산
단면적 ( A ) 는 폭 ( w ) 와 높이 ( h ) 의 곱으로 주어집니다:
[
A = w h
]
따라서 단면적 변화율을 계산하면:
[
\frac{\Delta A}{A} = \frac{\Delta w}{w} + \frac{\Delta h}{h}
]
푸아송 비의 정의에 따르면:
[
\frac{\Delta w}{w} = -\mu \epsilon, \quad \frac{\Delta h}{h} = -\mu \epsilon
]
즉, 폭과 높이 방향에서 변형률에 비례하여 줄어드는 만큼 단면적도 줄어듭니다. 이를 합치면:
[
\frac{\Delta A}{A} = -\mu \epsilon – \mu \epsilon = -2\mu \epsilon
]
하지만 실제 계산에서는 절대값을 사용하여 방향성을 고려하므로:
[
\frac{\Delta A}{A} = 2\mu \epsilon
]
🔹 최종 결론
따라서, 단면적 변화율은 푸아송 비의 두 배만큼 변형률에 의해 변한다는 것이 바로:
[
\frac{\Delta A}{A} = 2\mu \epsilon
]
이 공식이 나오는 이유입니다! 😊
이해가 되셨나요? 혹시 추가적인 설명이 필요하면 알려주세요! 🚀✨
좋아요! 단면적 변화율 (\frac{\Delta A}{A}) 가 어떻게 (\frac{\Delta w}{w} + \frac{\Delta h}{h}) 가 되는지 정확히 설명해볼게요.
🔹 단면적 변화율의 개념
단면적 ( A ) 는 폭 ( w ) 와 높이 ( h ) 의 곱으로 표현됩니다:
[
A = w h
]
따라서, 단면적의 변화량 ( \Delta A ) 는 다음과 같이 미분하여 구할 수 있습니다:
[
\Delta A = (w + \Delta w)(h + \Delta h) – w h
]
이를 전개하면:
[
\Delta A = w h + w \Delta h + h \Delta w + \Delta w \Delta h – w h
]
여기서 ( w h ) 항이 상쇄되므로,
[
\Delta A = w \Delta h + h \Delta w + \Delta w \Delta h
]
🔹 상대 변화율로 변환
양변을 ( A = w h ) 로 나누면:
[
\frac{\Delta A}{A} = \frac{w \Delta h}{w h} + \frac{h \Delta w}{w h} + \frac{\Delta w \Delta h}{w h}
]
정리하면:
[
\frac{\Delta A}{A} = \frac{\Delta h}{h} + \frac{\Delta w}{w} + \frac{\Delta w \Delta h}{wh}
]
마지막 항 ( \frac{\Delta w \Delta h}{wh} ) 는 변형률이 매우 작은 경우 무시할 수 있으므로, 근사적으로:
[
\frac{\Delta A}{A} \approx \frac{\Delta h}{h} + \frac{\Delta w}{w}
]
이렇게 해서 단면적 변화율이 폭 변화율과 높이 변화율의 합으로 근사될 수 있는 것입니다! 😊
이해가 되셨나요? 혹시 더 궁금한 점이 있으면 추가 설명해 드릴게요! 🚀✨